서론

VAE의 조금 더 수학적인 부분에 대해서 알아보자.

최대우도추정

먼저 최대우도추정 (MLE)에 대해서 알아보고 시작하자.

최대우도추정은 샘플을 보고 그 샘플이 나왔을 분포(를 이루는 파라미터)를 추정하는 것이다.

우도

일단 ‘우도’가 무엇인지부터 정리하고 가자면, 우도는 가능도라는 이름도 있으며 영어로는 Likelyhood이다.

대충 정리하면 확률밀도함수의 y값이라고 볼 수 있다. 확률과는 다른 값이다.

왜 그거 있지 않는가. 다트를 던져서 어느 한 지점에 떨어질 확률은 언제나 정확하게 0이다.

연속확률분포라면 언제나 한 특정 사건이 일어날 확률은 0이다. 다만 구간에 대해 확률밀도함수를 적분해서 그 구간의 확률을 ㄱ할 뿐이지.

하지만 그래도 어떤 특정 사건이 일어날 정도가 어떤지를 비교하고 싶을 때 쓰는게 가능도다. 그래프의 y값이다.

우도를 곱하자

이 사이트에 근사한 그림이 있길래 가져왔다.

mle

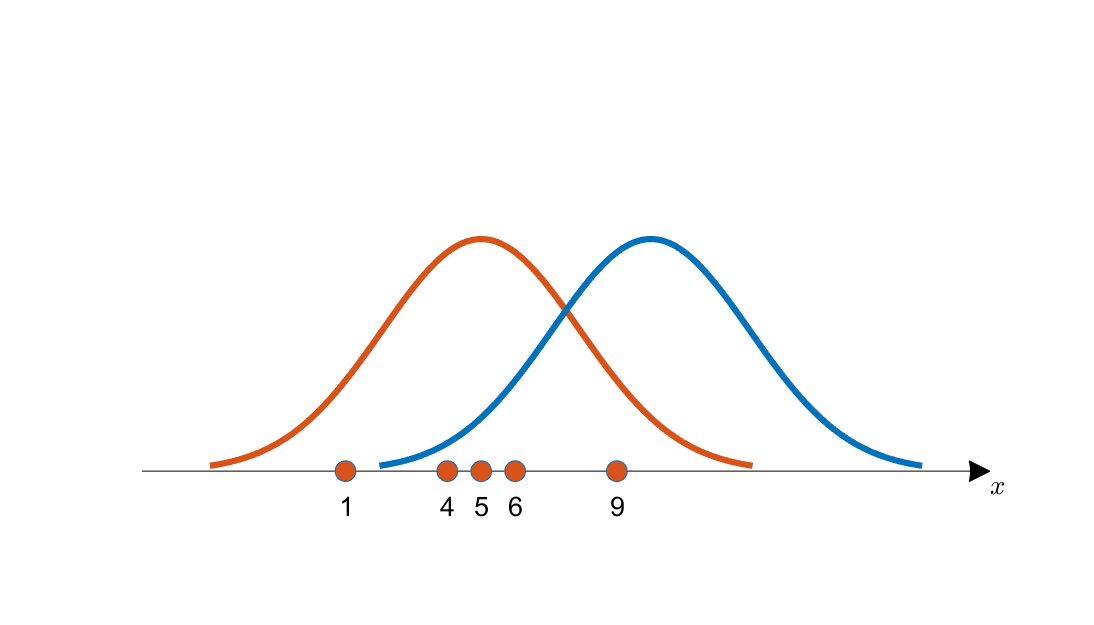
이 그림을 보자. 아래의 붉은 점들은 주황색 곡선에서 얻어졌을까, 아니면 파란색 곡선에서 얻어졌을까?

물론 파란색 곡선에서 샘플링을 했을 때에도 붉은 점들이 나올 수는 있다. 그것이 확률이니까.

하지만 주황색 곡선에서 얻어졌다고 해야지 좀 더 말이 되지 않을까?

주황색 곡선에서 얻어졌다고 하는게 더 말이 된다는걸 수학적으로 어떻게 이야기할 수 있을까?

mle2

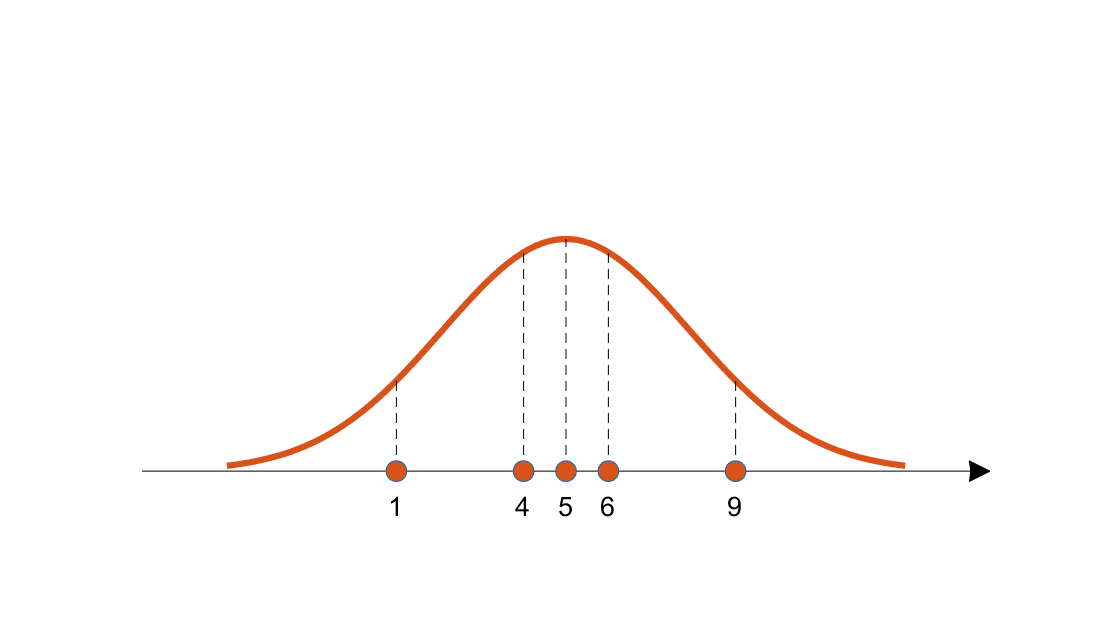
이렇게, 각 샘플의 우도를 전부 곱한 값이 (독립 추출이니까 곱한다고 한다.) 파란색 곡선보다 주황색 곡선에서 더 커진다는 것으로 ‘더 말이 된다’는걸 알려줄 수 있을 것이다.

그렇다면 각 샘플의 우도를 전부 곱한 값이 가장 큰 분포가 ‘최대 우도’를 가지고 있을 것이고, 그 샘플을 추출한 확률분포라고 말할 수 있을 것이다.

로그 우도 함수

이제 우도가 가장 큰 함수를 찾아보자.

$P(x|\theta) = \prod_{k=1}^{n}P(x_{k}|\theta)$

이 때 좌변이 최댓값이 되게 만드는 값을 세타의 근사값인 세타 햇이라고 불러도 되겠다.

전부 곱하는건 힘드니까 로그를 취해서 더하게 만들어주자.

$L(\theta|x) = P(x|\theta) = \sum_{k=1}^{n}log(P(x_{k}|\theta))$

그리고 ‘최댓값을 찾는다’고 했으니, 세타로 편미분해주자.

$\frac{\partial}{\partial\theta}L(\theta|x) = \frac{\partial}{\partial\theta}P(x|\theta) = \frac{\partial}{\partial\theta}\sum_{k=1}^{n}log(P(x_{k}|\theta))=0$

이제 여기다가 적당한 우도를 집어넣고 열심히 계산해보면 최대우도추정을 할 수 있다.

변분추론

또 이게 중요한 파트 같다. (지금 보면서 공부하고 있는 페이지는 여기고, 여기서도 변분 추론에 대해 여기로 링크를 걸고 있다.)

P(Z	X) (VAE의 예로 들면 이미지에서 잠재변수를 끌어내는… 확률분포라고 해야 하나…?)가 구하기 말도 안되게 어려울 때, 이를 Q(Z) (보통 정규분포같이 다루기 쉬운 확률분포)로 근사하고, 이를 KL 다이버젼스 등을 통해 학습하는 방식이다.

헷갈려서 적어두는건데, 모델이 학습하는 것은 확률 분포이다. 예컨데 VAE의 인코더가 학습하는 것은 P(잠재 변수

이미지)의 조건부 확률 분포이다.

그리고 또 이제 이 두 분포의 KL 다이버전스를 수학적으로 이챠이챠 잘 하는데…

결론만 말하면 q(z)와 p(z

x) 사이의 KL 다이버전스는 다음과 같다.

$D_{KL}(q(z)||p(z|x))=D_{KL}(q(z)||p(z))+\log p(x)+E_{z\texttildelow q(z)}[\log p(x|z)]$

또 이를 이렇게저렇게 잘 해주면 결국엔 log p(x)의 하한값을 구할 수 있어지는데, 이를 ELBO라고 부른다.

$\log p(x)\geq E_{z\texttildelow q(z)}[\log p(x|z)]-D_{KL}(q(z)||p(z))$

이는 최대우도추정에 쓰이게 된다.

공식들이 너무 많아

전부 공식들을 적어가면서 정리하느니 차라리 링크 주고 읽어보라고 하는게 나을 지경일 정도로 공식이 너무 많다.

그러니까 공식을 적지 않고 대충대충 해보자.

먼저 Decoder가 배우는 확률분포는 p(x

z)이다. 즉, z 잠재 변수가 주어졌을 때 이미지 x를 생성하는 확률 분포이다.

이는 정규분포로 가정된다.

이 모델을 구하기 위해서 최대우도추정을 해보려면 (어째서인지 조건부 부분을 없애고) Marginal log likelyhood를 계산한다. 원래 Marginal이라는게 그런 뜻으로 쓰였던 것 같다.

이 때 구하는게 log p(x)이기 때문에 위에 적어둔 공식이 쓰이게 된다.

여기에서 q(z)는 보통 단순한 정규분포지만, 데이터 x가 고차원일 때는 이렇게 하면 학습이 힘들다.

여기서는 q(z)의 파라미터를 x에 대한 함수로 둬서 해결한다고 한다.

한편 인코더도 변분추론을 도입해서 p(z

x)를 학습한다.

이를 위해 q(z)와 q(z

x)의 KL다이버전스를 계산해주게 되고, 이는 위의 식대로 된다.

이를 어떻게 열심히 정리하면 Loss 함수가 나온다 (?)

아무튼 최종적으로 나오는 공식은 다음과 같다.

Reconstruction Error와 Regularization으로 나눠볼 수 있는 이 공식에 대한 설명은 저번에도 했지만…

Reconstruction Error쪽은 잘 보면 교차 엔트로피다. 실제 구현 시에는 x와 재구성된 x 사이의 binary 교차 엔트로피를 계산한다.

Regularization쪽은…. 으음, 아직도 잘 모르겠다. 몇 시간이나 이걸 보고 있었는데…

아무튼 오늘은 여기까지.

다음 시간

드디어 diffusion model에 대해 다시 알아보자. 조금 더 뭔가 알 수 있는게 있지 않을까.