서론

배운건데 까먹었다.

다시 복습해보자.

다변수 함수

일단 간단하게 짚고 넘어가자.

다변수 함수는 매개변수가 여러 개 있는 함수이다.

f(x, y)같은 놈 말이다.

그 외에 딱히 언급해야 할 것은… 없는 것 같다.

극한

원래 함수의 극한의 정의는 소위 ‘입실론-델타 논법’이라고 해서 ‘모든 0보다 큰 ε값에 대해 어떤 δ값이 존재하여 (어쩌고 저쩌고’였다.

조금 더 자세히 살펴보자.

$\lim _{x \rightarrow a} f(x) = L$

이런 극한이 있다고 하자.

어떻게 글로 표현하는걸 잘 못해서 그림으로 그려봤다.

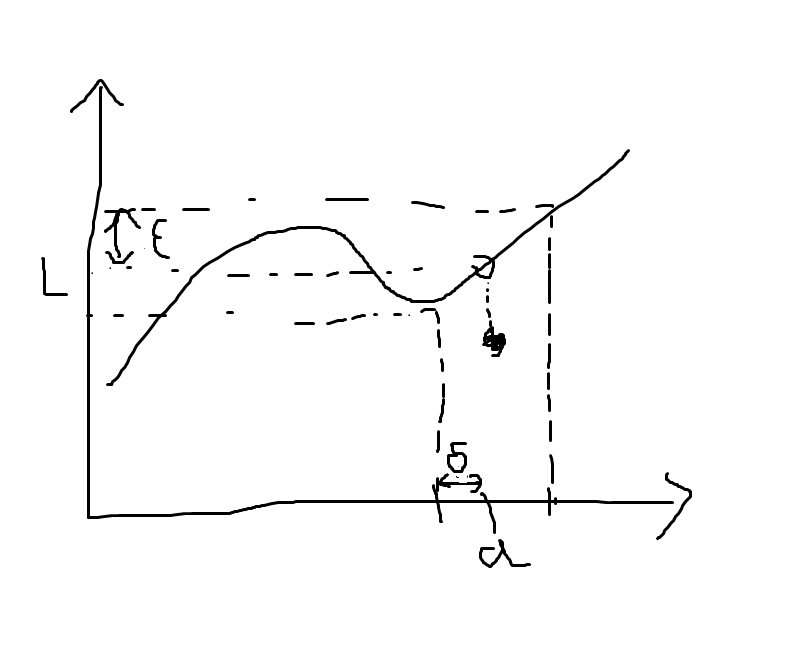
epsilon-delta

입실론-델타 논법은 여기서 ‘a 주변 δ거리 안에 x가 있다면 그 f(x)는 L 주변 ε거리 안에 있다’고 한다.

위 문장의 ε값이 무엇이던 상관 없이, 어떤 특정한 δ값을 구할 수 있다면, 위 극한이 성립하게 된다.

공식으로 나타내면 다음과 같다. (위키백과에서 발췌)

예전에는 이런거를 보면 정신이 아득해졌는데, 최소한 지금은 아득하다가도 조금 보다 보면 알 것 같은 느낌이 든다.

아무래도 수학이라는건 말 드럽게 못하는 이과놈들이 자기 생각을 표현하기 위한 방법인 모양이다.

(위 공식에서 E는 함수 f의 정의역이다.)

공식 이해하기?

그래도 위 공식이 잘 이해가 안되면 한번 뜯어보자.

앞쪽 한정자들 (뒤집어진 A하고 E들 나오는 부분)은 일단 무시하고, 화살표 있는 부분만 보자.

$0 < |x - a| < \delta \Rightarrow |f(x)-L| < \epsilon$

이 부분은 쉽다.

a값하고 L값은 정해진 값이니까 그렇다고 치고, 지금은 x값이 ‘정의역 내의 모든 값’이라는 것만 생각해보자.

x값은 정의역 내의 모든 겂인데, 이제 공식의 화살표 앞쪽에서 필터링에 들어가게 된다.

a하고 거리가 δ 이내인 x값이 아니라면 위 공식하고 상관이 없어지게 되기 때문에, x값이 a와 일정 거리 내의 값들로 한정된다.

즉 공식 뒷부분의 x는 ‘정의역 내의 모든 값’이 아닌, ‘a와 δ보다 적게 떨어진 모든 값’으로 생각하면 된다.

공식 뒷부분은 그렇게 한정된 x를 전부 f에 넣어본다. 이 때 나온 모든 f(x)값이 L과 ε 거리 안에 있다면, 위 공식은 성립한다.

그러면 공식 앞부분에 붙어있는 한정자는 무슨 뜻일까?

$\forall \epsilon >0, \exists \delta >0, \forall x \in E:$

x에 대한 이야기는 이미 했다. 정의역 내에 있는 모든 x에 대하여- 라는 뜻이다.

한정자가 어려운 이유는 순서가 중요하기 때문이다.

한정자의 순서에 대해서

어찌 이야기가 조금 새고 있는 것 같긴 한데…

이런 식으로 생각해보자. 흔히 나오는 예시다.

∀x∈People, ∃y∈People Loves(x, y) 와

∃y∈People, ∀x∈People Loves(x, y)

이 두 식의 차이다.

앞쪽은 ‘모든 사람은 그 사람이 사랑하는 어떤 사람이 있다’(= 사랑하지 않는 사람은 없다)라는 뜻이고,

뒤쪽은 ‘모든 사람이 사랑해주는 어떤 사람이 있다’는 뜻이다.

수학자들은 자연어가 이해하기 어렵다고 불평을 하기는 하는데, 아무래도 자연어로 치환해서 생각하는게 편리한 이상 어쩔 수 없는 일이다.

어떻게 생각하는게 좋을까? 한번 이렇게 생각해보자.

앞에 오는 것을 먼저 ‘고정한다’고 생각해보자.

예컨데 ∀x∈People, ∃y∈People Loves(x, y)는 x를 먼저 고정하고, 즉 ‘모든 사람에 대해 다음 문장이 성립한다’를 먼저 둔 다음에, y를 고정한다.

그렇기에 ‘모든 사람에 대해, 그들은 누군가를 사랑한다’라는 뜻이 된다.

반면 ∃y∈People, ∀x∈People Loves(x, y)는 y를 먼저 고정한다. 즉, ‘어떤 사람이 존재하여 다음 문장이 성립한다’가 먼저 나온다.

그렇기에 ‘어떤 사람이 있는데, 모든 사람이 그를 사랑한다’라는 뜻이 된다.

한정자의 순서에 대해서는 이 정도로 정리하면 될 것 같다.

다시 돌아와서

$\forall \epsilon >0, \exists \delta >0, \forall x \in E:$

이 한정자를 분석해보자.

ε값이 먼저 정해지고, 그 다음에 δ값, 마지막으로 x값이 정해진다.

즉,

ε값이 무엇이든 상관 없이,
어떤 δ값이 존재하고,
거기에 끼워맞출 수 있는 x값이 무엇이든 상관이 없다

순서가 된다.

뭐 아무튼 입실론-델타 관련된 이야기는 이 정도면 될 것 같다.

다변수 함수의 극한

이 이야기를 장황하게 한 이유는 다변수 함수의 극한을 정의하기 위해서인데…

δ를 ‘거리’라고 했었다. (ε도 그렇고.)

δ는 정의역에 붙는 ‘거리’이기 때문에, 정의역의 숫자가 둘이 됐다면 어떻게 해야 할까?

숫자 두 개를 가지고 거리를 계산하는 방법, 즉 유클리드 거리다. (아니면 컴공이고 하니까 L2 norm이라고 할까)

3차원은 손그림으로 어떻게 커버가 안되는 영역이니까, 지금 찾아보고 있는 웹사이트에 나온 이 그림을 보자.

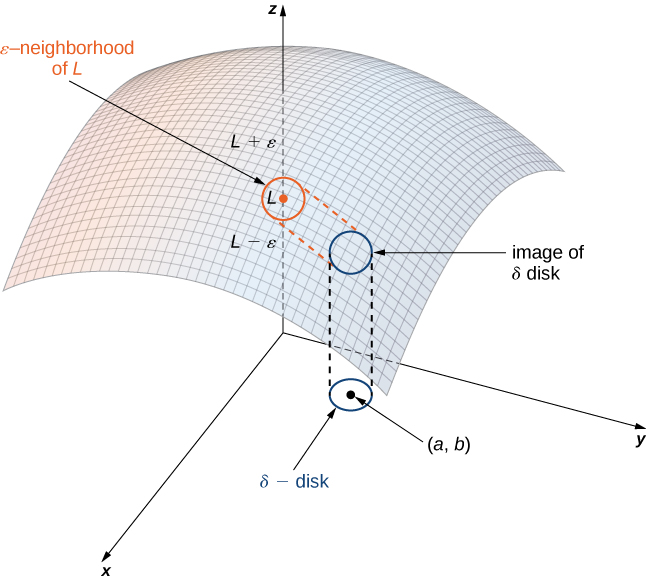
$epsilon-delta-3d$

이렇게, 똑같은 입실론 델타이지만 델타가 단순한 뺄셈에서 ‘거리’로 바뀐 형태가 다변수 함수의 극한이다.

편미분

편미분의 정의는 다음과 같다.

$\frac{\partial f}{\partial x}=f_{x}(x,y)=\lim_{h\rightarrow0}\frac{f(x+h,y)-f(x,y)}{h}$

뭐 복잡한건 아니다.

다변수 함수의 미분 가능성

다변수 함수의 미분 가능성은 이렇게 정의된다.

$f(x,y)=f(x_0,y_0)+f_x(x_0,y_0)(x-x_0)+f_y(x_0,y_0)(y-y_0)+E(x,y)$

여기서 E는 다음과 같은 조건을 성립한다.

$\lim_{(x,y)\rightarrow(x_0,y_0)}\frac{E(x,y)}{\sqrt{(x-x_0)^2+(y-y_0)^2}}=0$

위쪽 식에서 E(어쩌고)를 뺀 부분의 공식은 접면의 공식이다.

x와 y는 해당 점 주변의 δ원반 내에 있는 모든 점이다.

위 공식을 말로 풀어서 설명해보면, ‘어떤 함수가 어떤 점에서 미분 가능하다’ 면 ‘그 점 주위의 δ원반 안에 있는 아무 점에 대해서, 그 점의 함수값과 (원래 미분 가능성을 구하려고 한) 점 위의 접면 함수 위의 값이 충분히 가까워야 한다’는 뜻이다.

‘충분히 가깝다’는건 위의 조건 공식을 따른다.

연쇄 법칙

그 다음은 연쇄 법칙의 증명인데… 솔직히 너무 길고 복잡하다.

(어떤 사이트에서는 아예 non-trivial하다면서 증명을 건너뛸 정도)

개인적으로는 엄밀한 증명보다 ‘왜 그렇게 되는지’에 대한 직관을 더 중요하게 생각한다.

…그래도 그건 다음에 알아볼까.

다음과 같다. z = f(x, y)가 있고, x = g(t), y = h(t)일 때, f를 t에 대해 미분하면

$\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x}\frac{dx}{dt} + \frac{\partial z}{\partial y}\frac{dy}{dt}$

즉 그냥 더하면 된다는 것이다.

다음 시간엔

왜 이게 저렇게 되는지에 대한 ‘직관적인’ 설명은 없을지를 찾아보자.

증명을 따라가는 것은 어렵고 복잡할 뿐만 아니라 제대로 된 직관을 제공하지도 못한다.