Optimizer - 2.옵티마이저: 발전
돌아보기
이전 글에서는 단순한 옵티마이저인 GD와 SGD에 대해 알아보았다.
이상적으로는 최솟값을 구하고 싶지만, 극솟값에 만족해도 괜찮다.
GD는 그라디언트가 작아지는 방향으로 움직이는 방법이다.
SGD는 미니배치를 나누는 방법이다.
들어가기 앞서
확실히 이해했는지는 모르겠지만, 일단 부딛혀보자.
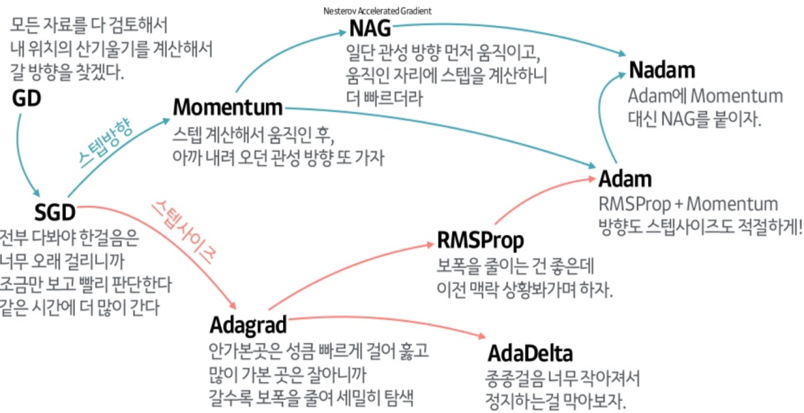
아, 참.
처음에 어디서 나온 이미지인지는 모르겠지만, 이런 글에 꼭 붙는 이미지에 이런게 있다.
나름 도움되는 이미지니까 한번 봐두고 시작하자.
Momentum
‘모멘텀’이라는 말은 원래 운동량이라는 뜻인데
왜인지는 모르겠지만 관성 비스무래한 무언가를 지칭할 때 정말로 많이 사용되는 말이다.
모멘텀 옵티마이저도 마찬가지로 관성 비스무레한 무언가를 사용한다.
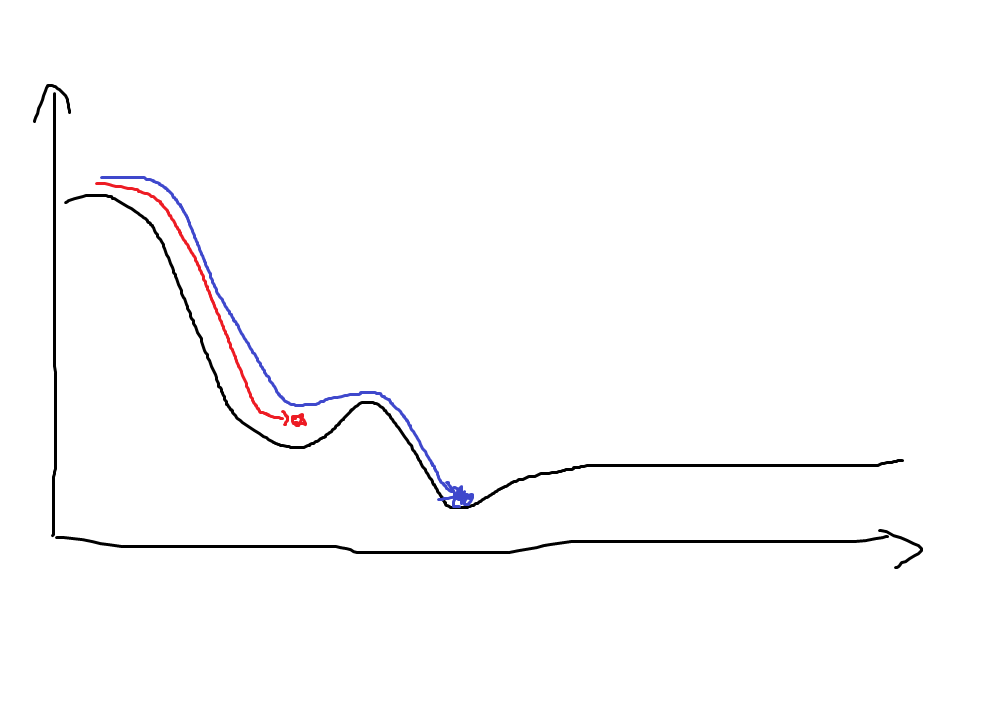
아마 이런 효과를 노린게 아닐까?
파란 색 선이 Momentum optimizer라고 하면, 얕은 극솟값 ‘우물’은 관성을 사용해서 빠져나올 수 있다.
공식을 보도록 하자.
V는 현재 ‘속도’를 의미하고, m은 얼마나 관성을 유지할 것이냐를 의미한다.
현재 가중치를 ‘위치’라고 생각해보자. 매 mini-batch를 학습시킬 때마다 (공식에는 표기되어 있지 않지만 mini-batch 기반 학습이다.) ‘위치’에 ‘속도’를 더해 그 다음 ‘위치’를 계산한다.
만약 관성이 아예 없다면 (관성계수가 0이라면) SGD와 다를 것이 없다.
관성의 요소를 도입해서, 현재 가는 방향으로 더 빠르게 가게 만든 Optimizer가 Momentum이다.
굳이 따지자면 그라디언트를 ‘가속도’라고 할 수 있겠다.
- 장점: 빠르게 학습이 가능하다.
- 장점: Gradient가 0이 되어도 관성으로 그 곳을 벗어날 수 있다.
- 단점: 학습 초기에 안 좋은 성능을 보여준다. (엉뚱한 방향으로 움직이기 시작하면 방향을 돌리기 힘들기 때문)
Nesterov Accelrated Gradient (NAG)
네스테로프… 사람 이름 같아 보인다. 찾아보니 러시아 수학자 유리 네스테로프가 개발한 방법인 모양이다.
대충 설명하면, Momentum 방식은 ‘내가 지금 서 있는 곳의 가속도’를 사용하는데, 그러다 보니 최적의 위치를 지나칠 위험이 있다.
그래서 대신 ‘도착 예정 지점 쯔음의 어딘가의 가속도’를 사용한다.
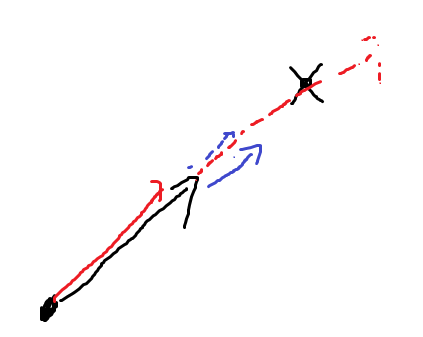
대충 그린 손그림이지만, 이런 상황을 생각해보자.
빨간 색은 기존 Momentum, 파란 색은 NAG이다.
최적의 위치를 지나칠 위험은 물론 NAG에도 있지만, Momentum에 비해 훨씬 덜할 것이다.
공식은 Momentum과 비슷하다.
Momentum 공식과의 차이점은 Loss(F()) 안쪽이다.
- 장점: Momentum과 장점을 공유한다.
- 장점: Momentum보다 제동이 빠르다.
- 단점: Momentum과 단점을 공유한다.
Adaptive Gradient (Adagrad)
적응형 그라디언트라고 해야하나?
컨셉은 이렇다. ‘내가 아무데나 떨어졌으면 어느 방향으로든 많이 바뀌어야지 극솟값이던 최솟값이던 도착하지 않을까’ 하는 마음을 전제로 해서,
‘즉 내가 이쪽 방향으로 거의 움직인게 없다면 이쪽 방향으로 더 많이 움직여야 하지 않을까’ 하는 것이다.
반대로 말하면, 지금껏 많이 변한 방향은 그만큼 적게 움직이게 만드는 방법이 AdaGrad이다.
수식으로 들어가기 앞서, 한번 생각해보자. 어떻게 하면 ‘지금껏 얼마나 변했는지’를 알 수 있을까?
당장에 떠오르는건 처음 시작한 위치를 기억해 두는 것이다.
현재 위치하고 처음 시작한 위치를 비교하면 얼마나 움직였는지 알 수 있지 않을까?
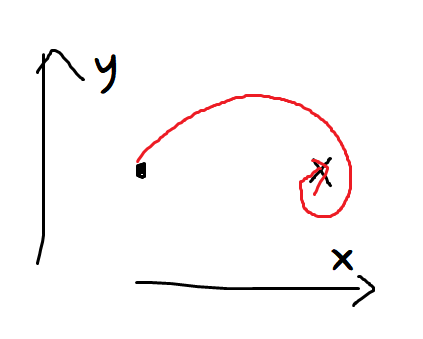
으음, 이런 예를 보자.
점에서 시작해서, X 위치에 도착하기까지 간 궤적을 그린 그림이다.
x좌표가 물론 많이 움직였긴 했지만, y좌표도 꽤 많이 변했었다.
하지만 처음 시작한 위치와 비교하기만 하면 y좌표는 전혀 변하지 않았다.
이 상황에선 y좌표도 많이 변했다고 해줘야 하지 않을까?
이 상황에서 y좌표가 쌩쌩하게 움직였다가는 원치 않은 곳으로 빠지지 않을까?
‘그러면 매 스탭마다 얼마나 움직였는지를 다 더하면 어떨까?’
역시 똑같다. +-해서 0이 되니까, 이런 상황에서는 별 도움이 안된다.
나는 아직도 잘 이해를 못하겠지만 수학자들은 이럴 때 절대값보다 제곱을 선호한다.
매 스탭마다 얼마나 움직였는지를 제곱해서 쭉 더해주면 ‘얼마나 많이 변했는지’를 알 수 있을 것이다.
물론 더할 때 제곱해서 더했으니 나중에 다시 계산할 때엔 제곱근을 취해주는 것도 잊지 말아야 하고.
수식으로 정리하면 다음과 같다.
조금 뭐가 많은데 천천히 뜯어보자.
무엇보다 ε이 보이는데, 이건 뭘까?
너무 G가 작으면 분모가 0이 되어버릴 수 있다. 이를 방지하기 위한 작은 값이다.
Adagrad는 적게 움직인 파라미터는 큰 학습률을, 많이 움직인 파라미터는 작은 학습률을 가지게 한다.
참고로 그라디언트가 벡터이기 때문에 G 역시 벡터이다.
그라디언트 벡터의 값에 따라 각 파라미터마다 다른 값이 적용되게 된다.
(눈치챘을지 모르겠지만 방향과 파라미터 등은 같은 뜻으로 쓰이고 있다.)
- 장점: 파라미터마다 필요한 만큼의 학습률을 가질 수 있다
- 장점: 학습이 별로 되지 않은 방향을 빠르게 학습시킬 수 있다.
- 장점: 학습이 적당히 된 파라미터는 학습률이 줄어들어 제대로 제동할 수 있다.
장점이 많기도 하고, 꽤 빠른 학습을 보여주면서, 동시에 제동도 괜찮은 방법이지만, 조금만 곰곰히 생각해보면 알 수 있는 치명적인 단점 또한 있다.
- 단점: 학습이 오래 진행되면 점점 변화가 일어나지 않다가 결국에는 멈추게 된다.
다음 시간
RMSProp이나 Adadelta, 그리고 Adam 등 다른 방법에 대해 공부해볼 것이다.